Chapter 1: Introduction to Sangaku and Geometry

Sangaku puzzles, known for their intriguing geometric properties, are a delightful exploration of mathematics. In this article, we will delve into a puzzle reminiscent of Sangaku, employing squares and a triangle for a unique challenge.

We have previously explored various Sangaku problems, and I trust you found them engaging. Today's focus will be on a problem that involves three congruent squares symmetrically inscribed within an equilateral triangle. Your task is to express the side length of the outer triangle in terms of the square's side length. Additionally, you should demonstrate that the area of the outer triangle is approximately twenty times that of the inner triangle.

To assist you, here’s a hint: consider utilizing some basic trigonometry. I encourage you to pause here, grab some paper and a pen, and try to work through it. Once you're ready, continue reading for the solution!

Section 1.1: Setting Up the Problem

Let’s assume each square has a unit length of 1. Since the equilateral triangle has angles of 60 degrees, bisecting it yields an angle of 30 degrees.

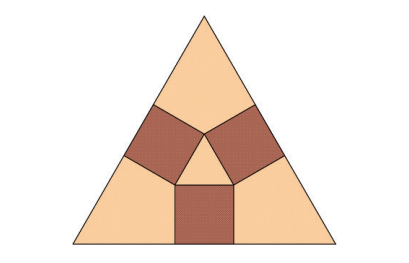
Next, focus on the right triangle located at the bottom right corner. The opposite side measures 1, corresponding to the unit length of the square.

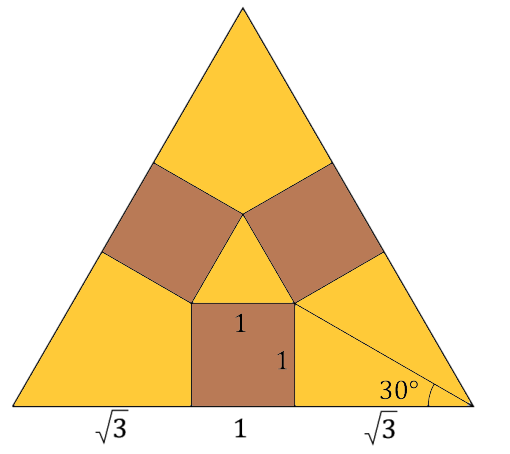
Section 1.2: Solving for Side Length

By applying the tangent function, we can determine the length of the adjacent side in the triangle.

Subsection 1.2.1: Calculating the Total Length

To find the total side length of the equilateral triangle, we will sum the lengths of the three segments.

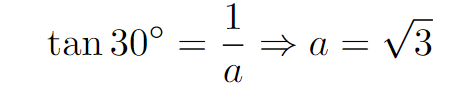
Now, how can we prove that the area of the outer triangle is about twenty times larger than that of the inner triangle? It's important to notice that the inner triangle is, in fact, another equilateral triangle with a side length of 1. To ascertain their area ratio, we simply calculate the square of the ratio of their side lengths.

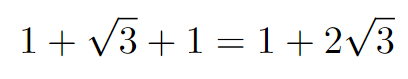
Chapter 2: Understanding Area Ratios

To conclude, the outer triangle's area is indeed approximately twenty times greater than that of the inner triangle.

The first video, "A Sangaku Puzzle (Japanese Temple Problem)," provides a deeper insight into similar problems and methods to solve them.

The second video, "A Quick and Easy Sangaku Puzzle," offers a straightforward explanation of solving such puzzles.

What were your thoughts while tackling this problem? I’d love to hear your insights—feel free to comment below!

Math Puzzles Collection

Explore the best math puzzles available on Medium, covering various topics like Algebra, Geometry, and Calculus. Share these with your friends!

Thank you for taking the time to read this article! If you found it valuable, please show your appreciation by clapping.