# Understanding Newcomb’s Problem: The Dilemma of Choices
Written on
Chapter 1: The Arrival of Omega and the Two Boxes
Imagine a lively gathering among friends, engrossed in discussions about intriguing thought experiments. Suddenly, an unusual figure steps forward.
“Hello everyone,” introduces the being. “I am Omega, and I have brought two boxes with me.”
Omega places two boxes on the table, marked A and B.
“Box A is open and contains $1,000. Box B, however, holds a mystery; it is sealed, and I will determine its contents shortly. One of you will soon be invited to participate. You will face a choice: you can either take only Box B, which is known as one-boxing, or you can opt for both boxes, referred to as two-boxing.”
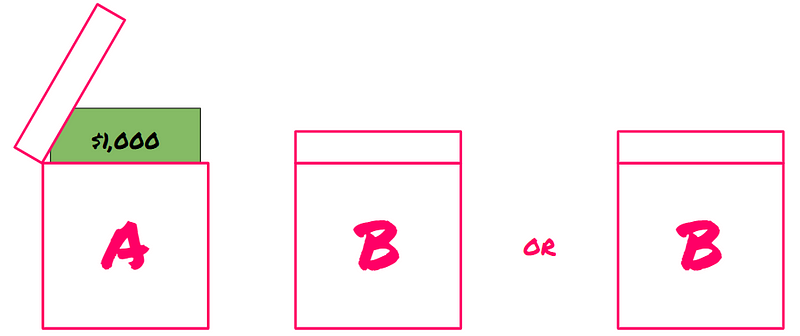
An Intriguing Dilemma
“I will make a prediction about your choice,” Omega continues. “I am exceptionally skilled at anticipating human behavior in this scenario. If I predict that you will choose to two-box, then Box B will be empty. Conversely, if I foresee you opting for one-boxing, I will fill Box B with $1,000,000.”
“I possess both empty envelopes and those containing $1,000,000, and they appear identical, making it impossible for the player to know what is inside Box B. After I finalize my prediction and place an envelope in Box B, I assure you that I will not alter the contents.”
Omega invites Carl to participate. Eagerly, Carl accepts the challenge. Following through on the promise, Omega places an envelope — either empty or containing $1,000,000 — in Box B.
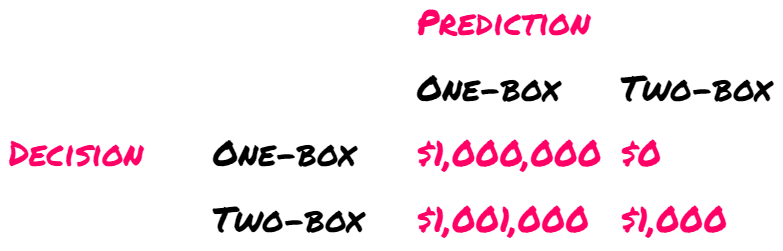
Carl reflects: “The past is unchangeable; my choice of one-boxing or two-boxing does not influence whether Box B has $1,000,000; that is already determined. I desire the $1,000,000, but that’s beyond my control. If Box B is empty, two-boxing yields $1,000, while one-boxing results in nothing. If Box B contains $1,000,000, two-boxing gives me $1,001,000, whereas one-boxing provides only $1,000,000. In both scenarios, two-boxing is the better option, so I will choose to two-box.”
Consequently, Carl opts for two-boxing — an outcome Omega accurately predicted. Carl opens Box B only to find an empty envelope. While he still receives $1,000, his consolation is minimal.
Omega invites more participants. Some choose to two-box, and others one-box. Strikingly, Omega’s predictions prove correct each time: all two-boxers leave with just $1,000, while every one-boxer walks away with a hefty $1,000,000.
Next, Omega invites Eve to play. As before, Omega places an envelope in Box B.
Eve muses: “Given that Omega has accurately predicted every outcome, her forecasting appears credible. Since one-boxing has been considerably more profitable than two-boxing thus far, I will choose to one-box.”
To no one's surprise, Eve uncovers $1,000,000 within Box B.
“If only you had two-boxed!” remarks Christine. “Had you chosen two-boxing, you would have walked away with $1,001,000. Carl's decision to two-box was unfortunate!”
Elliott argues: “It’s not just Carl; every two-boxer only received $1,000. Clearly, one-boxing is the superior option, given that every one-boxer won $1,000,000.”
“But you cannot change what has already happened!” counters Carter. “You seem to suggest that two-boxing directly leads to an empty Box B, while one-boxing results in $1,000,000 being placed inside it!”
So, who is correct? Carl presents a rational argument: two-boxing seems to guarantee an extra $1,000. Yet, Eve also makes a valid point as the historical data favors one-boxing.
A critical assertion of this discussion is that both Carl and Eve are mistaken in their reasoning, albeit in different ways. Additionally, there is a correct method to approach this dilemma.
Rest assured, subsequent chapters will delve deeper into the errors made by Carl and Eve, as well as the proper way to tackle this problem. But for now, we will explore key concepts that are essential for understanding Newcomb’s Problem, the formal name for this fascinating game.
Stay tuned for Chapter II. Thank you for engaging with this exploration!
If you wish to support Street Science, consider contributing on Patreon.
Chapter 2: The Coherence of Decision-Making
In this video titled "What Were You Thinking? Decision Theory as Coherence Test," Prof. Itzhak Gilboa discusses how decision theory can be viewed as a test of coherence in our thinking processes. He examines the implications of rational choice and the challenges posed by paradoxes like Newcomb’s Problem.