Euler's Insights: Exploring the Sums of Reciprocal Series
Written on
Chapter 1: Euler's Groundbreaking Discoveries
In 1735, the illustrious mathematician Leonhard Euler introduced his influential paper titled “De summis serierum reciprocarum” (On the Sums of Series of Reciprocals). In this work, Euler unveiled a universal formula for calculating the sum of these series:
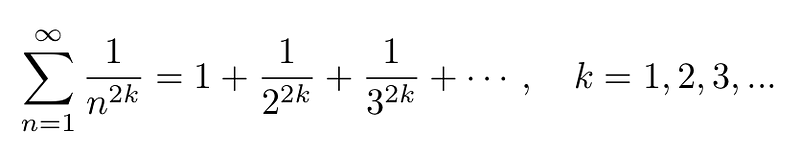
This remarkable approach has captivated mathematicians for centuries. Euler had already addressed the Basel problem in 1734, which serves as a foundation for extending this problem to any even exponent.

The initial three examples he derived are:
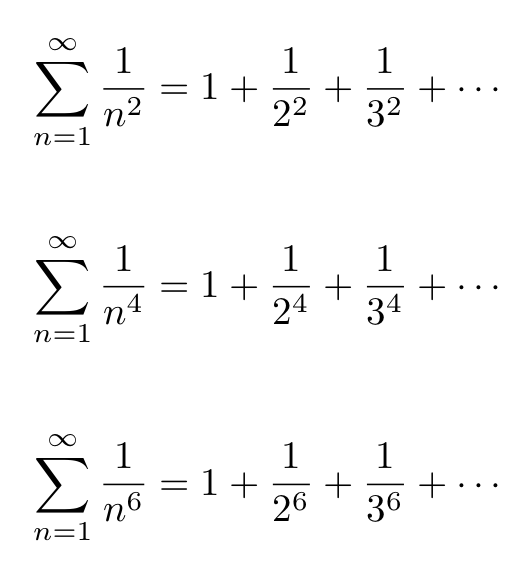
The first example corresponds to the Basel problem, previously solved by Euler the year before.

Before diving into Euler's profound proof, we must first clarify the concept of Bernoulli numbers.

These numbers were named after Jacob Bernoulli, who, along with Japanese mathematician Seki Kōwa, independently discovered them.
Understanding Bernoulli Numbers
The first step of the proof involves revisiting the concept of Taylor series. A Taylor series can be described as "a function's series expansion around a specific point." Given the complexity of Taylor series, we will focus solely on the expansion of the exponential function ( e^x ):
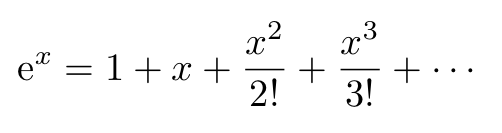
The radius of convergence ( R ) for ( e^x ) is ( R = infty ), indicating that the series converges for all values of ( x ).
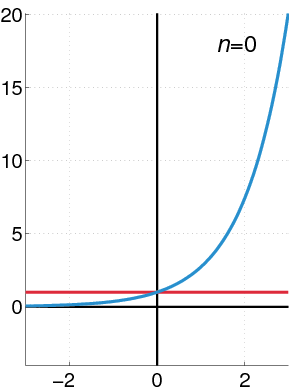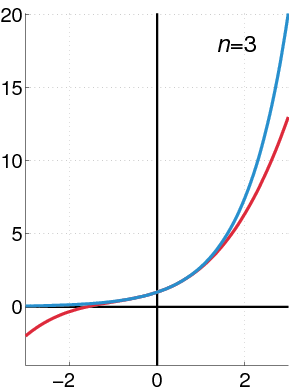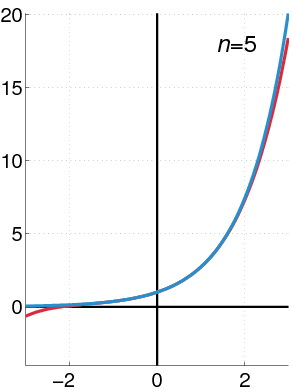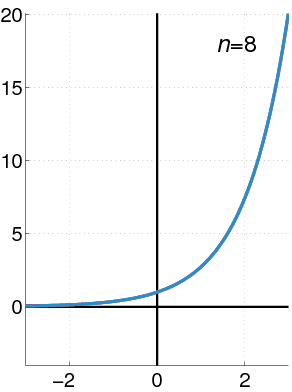
To derive the Bernoulli numbers, we perform two straightforward operations: first, we subtract 1 from both sides of the Taylor series and then divide by ( x ), leading us to:
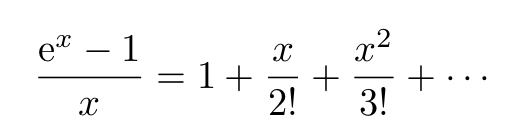
This equation holds for ( x neq 0 ). The Bernoulli numbers are subsequently defined by inverting this series:
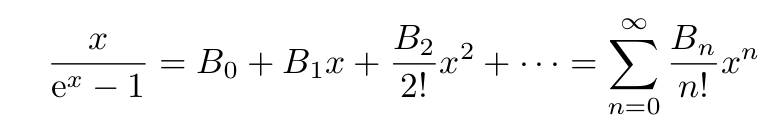
Using a clever mathematical approach, we can establish a product of these two equations, yielding a concise expression to compute the Bernoulli numbers directly:
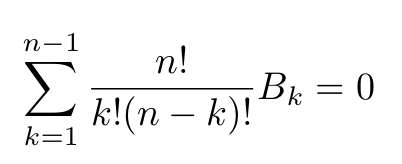
The first few Bernoulli numbers can be derived from this expression:
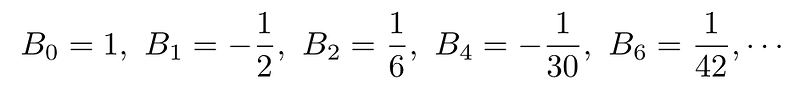
The Tangent Function and Its Power Series
Next, we will express the tangent of ( x ) using Bernoulli numbers. We start with the identity:
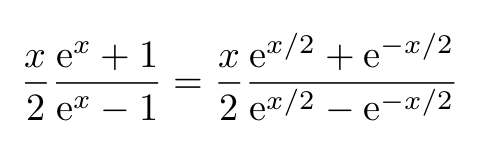
This leads us to:
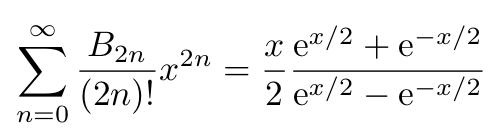
By substituting ( x ) on the right side of the equation with ( 2ix ) (where ( i ) is the imaginary unit), we get:
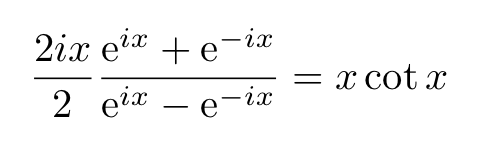
Applying the same substitution to the left side yields:
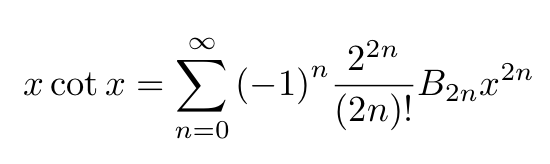
Utilizing the trigonometric identity, we can derive:
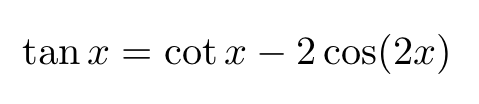
This ultimately leads us to the power series for ( tan x ):
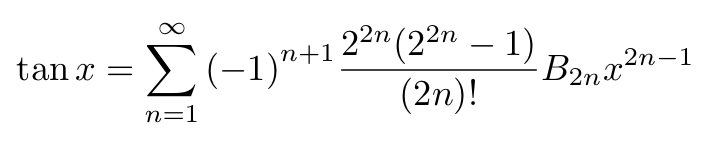
The Cotangent Function and Its Partial Fractions
In the concluding part of our proof, Euler utilized partial fractions to develop the following expansion:
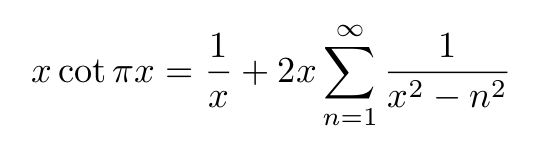
We can now compare the earlier equation with this new expansion, replacing ( x ) with ( pi x ). After some algebraic manipulations, we arrive at an elegant result:
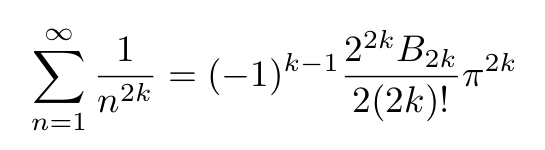
It is noteworthy that there is no analogous formula for odd exponents. For instance, the sum of the reciprocals of cubes results in a constant known as Apéry’s constant, approximately 1.20, but lacks a general formula like the one derived here. Perhaps a reader may eventually uncover such a formula!
For further exploration of mathematics and related subjects like physics, data science, and finance, feel free to visit my GitHub and personal website at www.marcotavora.me!