Understanding Matrix Traces: Definitions, Properties, and Derivatives
Written on
Chapter 1: Introduction to Matrix Traces
The trace of a matrix, commonly represented as tr(X) for any square matrix X, is a key principle in linear algebra that finds applications in various domains such as mathematics, computer science (including machine learning), physics, and engineering. This article will examine the definition, properties, and derivatives of the matrix trace, highlighting its importance and utility in different mathematical scenarios.
Vector and Matrix Notation

Vector Norms
In the realm of machine learning, numerous vector and matrix norms are employed for diverse modeling tasks. Among these, the L2-norm, also referred to as the Euclidean norm, is frequently used. For a vector x in an n-dimensional space, the L2-norm is calculated as the square root of the sum of the squares of its components, mathematically denoted as:

For both two-dimensional and three-dimensional vectors, intuitive examples can be illustrated. The L2-norm is widely utilized across various mathematical and computational fields such as optimization, machine learning, signal processing, and physics, owing to its geometric significance and mathematical attributes.
Inner Product
The inner product, often known as the dot product or scalar product, is a mathematical procedure that takes two vectors of equal length and yields a single scalar value. We will begin by exploring some fundamental concepts related to the inner product.

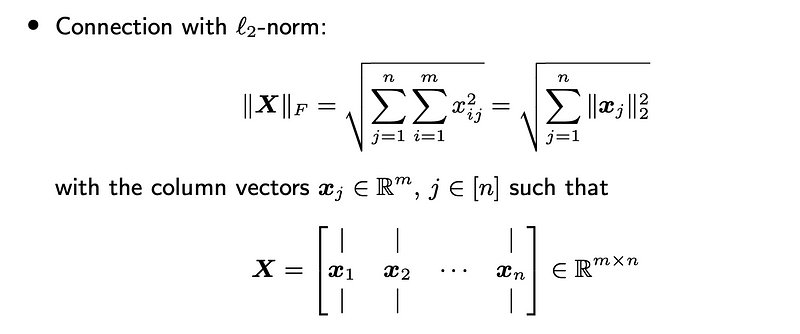
Frobenius Norm
The Frobenius norm, sometimes called the Euclidean norm or matrix norm, serves as a measure of the size or magnitude of a matrix. For a matrix X with dimensions m×n, the Frobenius norm is defined as the square root of the sum of the squares of all its elements.

Additionally, a connection can be established between the Frobenius norm and the L2-norm.
Definition of Matrix Trace
The trace of a square matrix A is defined as the total of its diagonal elements.

Properties of Matrix Traces
Several critical properties characterize matrix traces:
- Property 1: tr(X + Y) = tr(X) + tr(Y)

- Property 2: tr(XY) = tr(YX)

- Property 3: Connection with Frobenius Norm
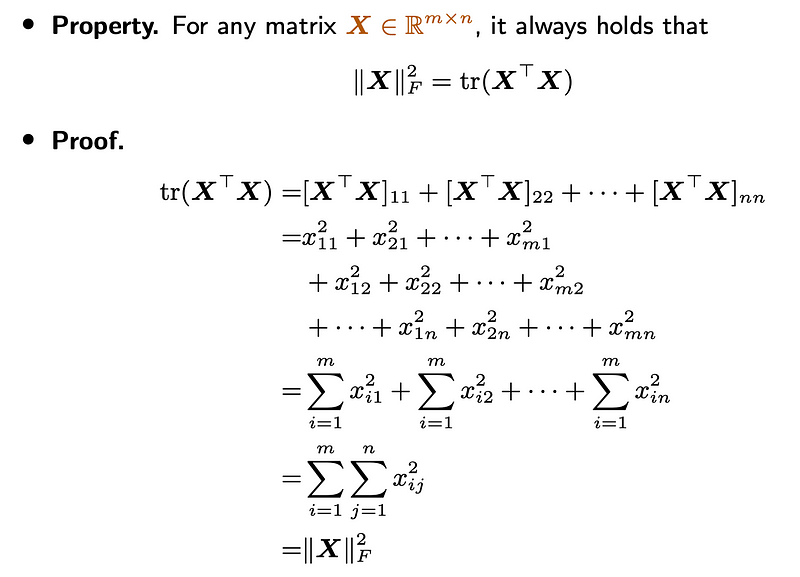
- Property 4: tr(X, Y) = tr(X^T Y)

Derivatives of Matrix Functions
In matrix analysis, determining the derivative of a function is crucial. Below, we introduce the basic definitions of derivatives.

We will further explore functions built on matrix traces and explain how to derive their derivatives.

Application: The Orthogonal Procrustes Problem
The Orthogonal Procrustes Problem (OPP) is a mathematical challenge in linear algebra and optimization, named after the Greek mythological figure Procrustes, known for altering his victims to fit an iron bed. In mathematical terms, this problem involves finding the optimal orthogonal transformation (rotation and/or reflection) to best align two sets of points or matrices.

Conclusion
The matrix trace is a multifaceted and potent concept within linear algebra, providing insights into the structure and properties of matrices. Grasping its definition, properties, and derivatives enhances one's understanding of linear algebra and facilitates its application in various mathematical and computational tasks, from matrix manipulation to optimization and machine learning.
In forthcoming articles, we will delve into advanced topics related to matrix traces, including their applications in eigenvalue problems, matrix exponentials, and differential equations, further exploring their significance in mathematics and beyond. Keep an eye out for more insights into this intriguing mathematical concept!
The first video discusses the derivative of a trace with respect to a matrix, offering valuable insights into this concept.
The second video covers determinants, derivatives, and traces, providing a comprehensive overview of these interconnected topics.