Chapter 1: Introduction to the Problem

In this section, we tackle a problem featured in the 2024 Bulgarian Winter Tournament, a challenging task set by talented students from Bulgaria. Before diving into the solution, it's worth attempting the problem yourself; you might surprise yourself with your progress!

Often, in problems like this, considering "roots of polynomials" can be beneficial. Although this concept may be unfamiliar to some, the critical approach involves making substitutions such as ( s = x + y ) and ( t = xy ). This allows us to reformulate the equations in a more manageable form.

Expanding the first equation gives us:

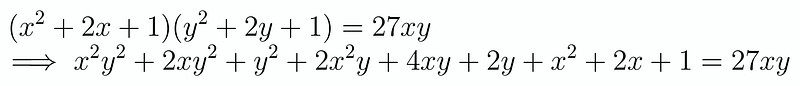
Next, we aim to express this equation using our variables ( s ) and ( t ). Remember that ( s^2 = x^2 + 2xy + y^2 ), so we can rewrite our equation as follows:

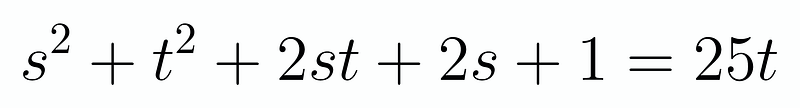
We'll apply the same strategy to the second equation. We intentionally avoided writing ( s^2 + 2st + t^2 ) as ( (s+t)^2 ) because our goal is to eliminate one of the variables. The second equation can thus be represented as:

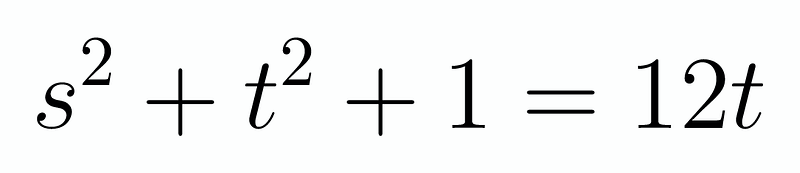
Subtracting one equation from the other helps us establish a relationship between ( s ) and ( t ):

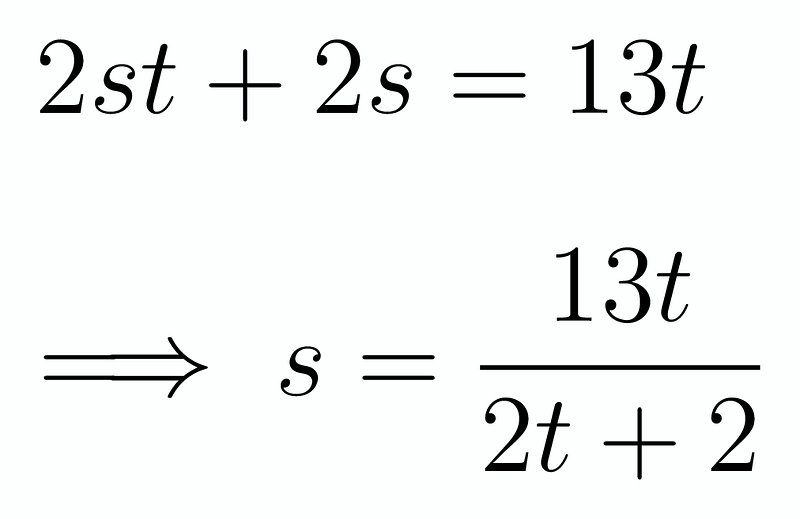
At first glance, this may not appear useful, but it indeed offers valuable insights. We can substitute this back into the second equation, which is simpler, resulting in:

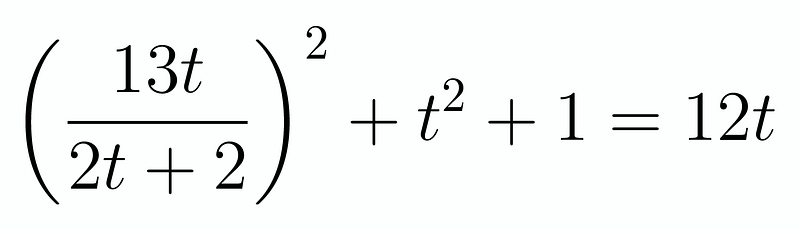
After expanding this expression and multiplying by the denominator, we arrive at a quartic equation:

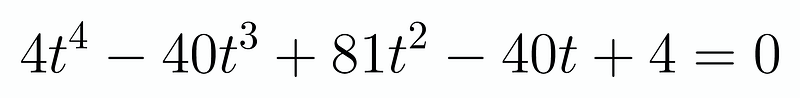
However, solving quartic equations can be quite complex. We might try substituting different values for ( t ) to find factors, but it appears that none fit. Instead, we can employ a technique we've seen in other scenarios. Notice the symmetry in the coefficients; if you were to "mirror" their positions, you would obtain the same quartic. This suggests a substitution of the form ( z = t + frac{1}{t} ), allowing us to transform the expression into a quadratic format.

You may wonder how this substitution is beneficial. The crucial step is to divide the entire equation by ( t^2 ), revealing the underlying structure:

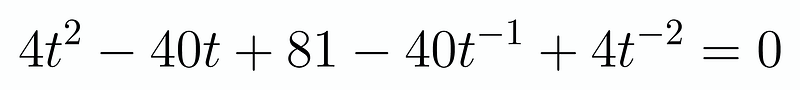
Next, we simplify further:

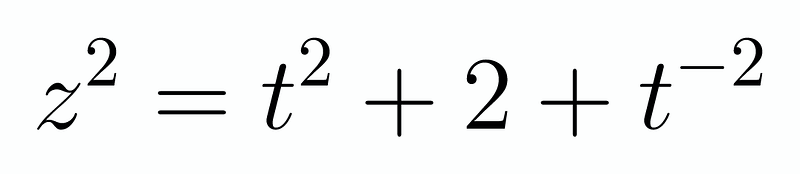
This leads us to the following equation:

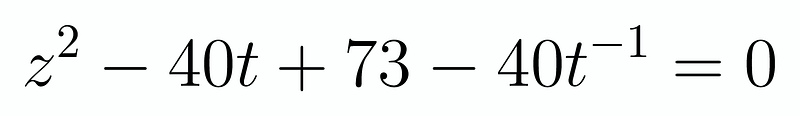
Repeating this process, we find that our equation transforms into:

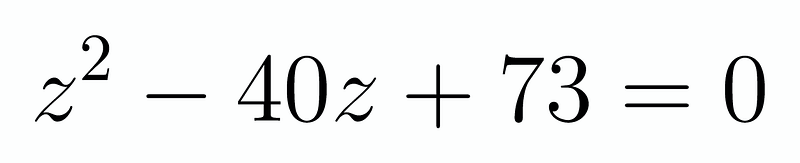
Using the relationship ( z = t + frac{1}{t} ), we can derive another quadratic equation. Notably, ( zt = t^2 + 1 ), leading us to obtain four solutions for our quartic equation. While we will skip the tedious algebra, we ultimately arrive at:

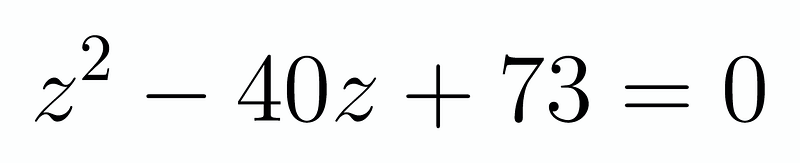
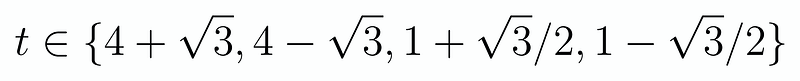
Now, we substitute these values back into the formulas for ( s ) and solve the straightforward simultaneous equations of the forms ( xy = a ) and ( x + y = b ) (which also leads to a quadratic, unfortunately). After all this effort, we discover eight potential solutions for ( x ) and ( y ), noting that if ( (x, y) ) is a solution, then ( (y, x) ) is also valid:

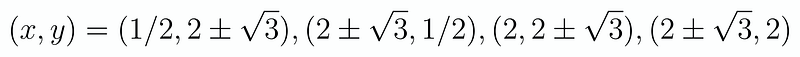
If there's one takeaway from this exercise, it's the importance of remembering your quadratic formula from middle school!

I genuinely hope that some readers have found a more elegant solution to this problem, as it doesn't seem optimal despite yielding satisfactory results. Feel free to share your thoughts in the comments below!

Explore the strategies used to solve complex simultaneous equations in the 2024 Bulgarian Winter Tournament by watching this insightful video!