Chapter 1: Understanding Graham's Number

Before diving into the incredible concept of Graham’s number, let’s first grasp the staggering scale it represents.

To conceptualize the smallest meaningful length in the universe, consider the Planck length. This is the length at which conventional ideas of distance begin to lose their significance, akin to the pixels in a digital image. A Planck volume, which is derived from cubing the Planck length, is so minuscule that it is estimated there are vastly more Planck volumes within a cubic meter than there are cubic meters in the observable universe.

To illustrate just how tiny a Planck length is, think of dividing the diameter of a proton by a hundred billion billion! This size is virtually unfathomable, and our understanding of nature at this scale remains limited.

Now, envision writing numbers using Planck-length characters. If you were to write a number containing Avogadro's number of digits in this font, it would occupy merely one-hundredth of an atom's diameter. Graham's number is so immense that it is impossible to represent all its Planck-sized digits even if the entire observable universe served as your writing medium.

In fact, the size of Graham's number is such that even the count of its digits cannot be expressed using the Planck font. This brings us to the question of its significance in mathematics—what makes Graham's number remarkable?

How Graham's Number is Used

Graham's number holds the title of the largest number that has been utilized constructively in a mathematical proof. To understand its application, we should explore its roots in Ramsey theory, a branch of combinatorics focused on the study of substructures derived from a complete structure, particularly concerning hypercubes.

This might sound like a concept from a science fiction narrative, but hypercubes are quite real in mathematics. They represent cube-like forms in dimensions beyond the standard three we experience.

For example, a circle is a one-dimensional shape in two-dimensional space, while the two-dimensional counterpart of a circle is a sphere, a shape we frequently encounter in everyday life—think of soap bubbles and sports balls. We can extend this notion to define spheres in higher dimensions, including three-dimensional cubes with eight vertices, and generally, an n-dimensional cube has 2^n vertices.

The vertices of an n-dimensional cube can be connected by edges, creating a complete graph. In the early 1970s, mathematicians Graham and Rothschild posed an intriguing question about these graphs.

They considered a complete graph formed from 2^n vertices on an n-dimensional hypercube, coloring the edges either red or blue. The central query was to determine the smallest dimension n such that any coloring would include at least one single-colored complete subgraph with four vertices lying in the same plane.

Graham and Rothschild established a significant theorem, leading to a special case that provided an astonishing upper bound for this problem.

The number they arrived at was not the ultimate answer but rather a number N that assured the actual answer lay between 6 and N, confirming the existence of such a dimension. Graham’s number, denoted as G, far exceeds N. This less stringent upper bound, credited to an unpublished work of Graham, was later brought to light by Martin Gardner in Scientific American in November 1977.

How to Write Down Graham's Number

To express Graham's number, we must introduce Knuth’s up-arrow notation, represented by the symbol ↑.

A single up-arrow signifies exponentiation (repeated multiplication), as shown in the following examples:

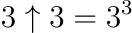
A double up-arrow indicates iterated exponentiation.

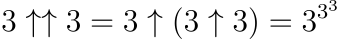
The notation illustrated on the right represents a "power tower" consisting of three 3s, which equates to 3² ↑ 3, yielding a value of 6 trillion. The triple up-arrow 3 ↑↑↑ 3 forms a power tower of 3s totaling 3 ↑↑ 3 times. This recursive definition continues endlessly.

To formally define Graham’s number, we adopt a recursive approach:

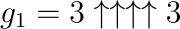
This is already an incomprehensible concept, as it is a power tower of 3s that reaches a height of 3 ↑↑ 3. Further, we can define:

Here, there are g_(n-1) arrows. If you’ve followed along this far, we can finally conclude that Graham’s number is defined as G = g_64.