Exploring the Geometry of Manifolds and Their Substructures
Written on
Chapter 1: Understanding Substructures in Mathematics
In the realm of pure mathematics, there is a significant focus on the characteristics of 'sub' objects. When a smaller object is part of a larger one, it is identified as a 'sub' object. For instance, within the set of all fruits, the collection of oranges represents a subset. Similarly, vector subspaces are subsets of larger vector spaces that also retain their own vector space properties.
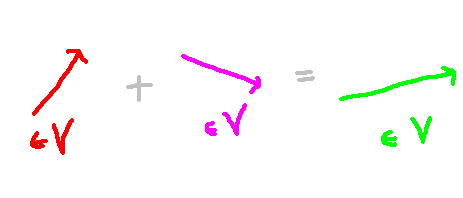
In vector spaces, when two vectors are combined, the result remains within that vector space. This raises intriguing inquiries about subspaces, particularly regarding which properties are passed down from the larger space. It is not a given that the attributes of the broader space will apply to the smaller one. For example, while the real line functions as a vector space—allowing for the addition and scaling of real numbers—the set {0, 1}, although a subset, does not qualify as a vector space. Scaling the number 1 by 2 removes it from the set, indicating that {0, 1} is a subspace but not a vector subspace.
Submanifolds and Their Embeddings
In mathematical physics, we often encounter a unique object known as a quotient space, which arises when one 'divides' a larger space by its subspace. This concept leads us to explore manifolds, submanifolds, and embeddings.
A submanifold can be defined as a subset of a larger manifold that itself behaves like a manifold. A manifold represents a smooth geometric structure that can be described with a set of coordinates. A classic example of a submanifold is a sphere situated within a three-dimensional space.
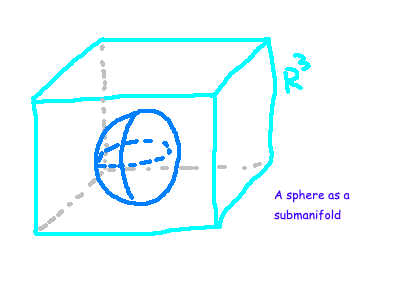
An embedding refers to the process of smoothly integrating a manifold into a larger Euclidean space. This brings to mind questions about cartography: Can we create a two-dimensional map that accurately reflects the distances between points on a spherical surface?
Submanifold Conditions
To understand what qualifies a manifold as a 'submanifold' of a higher-dimensional manifold, we must define the conditions under which this classification holds. This topic is complex and lacks straightforward answers. Additionally, we need to consider the conditions that make submanifolds 'smooth.'
We will define key concepts and examine the relationship between closed, proper immersions and embeddings, as well as introduce the idea of a homeomorphism with examples. A valuable reference for further reading on manifold embedding is "An Introduction to Smooth Manifolds" by J. Lee¹.
What Constitutes an Immersion?
To comprehend the mapping of a manifold into a subset of another, we need to construct a smooth map linking the two. The terminology used for transitioning between different manifolds proves useful here.
Let's denote a smooth map as ?:M?N between two manifolds. We can create a function that connects the tangent spaces of these manifolds. As previously mentioned, a tangent space is defined at a specific point in the manifold, consisting of vectors that reflect the rate of change of a function from various directions. Visualize it as a piece of paper tangent to a sphere.
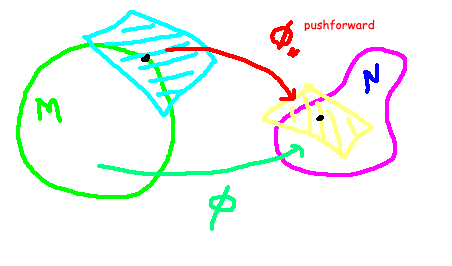
We can indeed construct such a map and induce a pushforward, ??, which maps between the tangent spaces of the manifolds at a specific point.
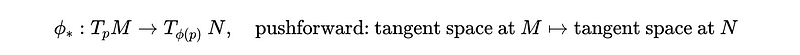
Assuming both M and N are finite-dimensional manifolds, they possess coordinate systems {x} and {y} at two distinct points. In this scenario, the components of ?? correspond to the Jacobian, which describes the transformation between coordinate systems. This mapping should be injective if the number of rows exceeds the number of columns, ensuring the pushforward does not compromise the original tangent space.
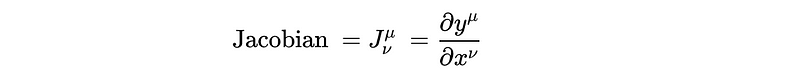
An embedding is characterized as an injective immersion. Injectivity implies that the function does not overlap with its target space. Furthermore, we require that the embedding acts as a homeomorphism onto its image, meaning it must map continuously to open sets, where the open sets of the image are determined by the topology of the target set. The continuity of the inverse function is also essential.
For instance, consider the mapping f: [0, 2?) to the unit circle. The function f is continuous, composed of two continuous functions, and is bijective. However, the inverse is not continuous, as there exists no small neighborhood around (0, 1) that is contained near 0.
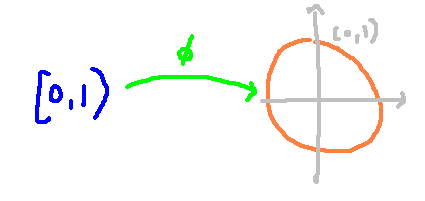
The neighborhood of (0, 1) consistently maps back to a slice containing two points: 0 and a point close to 2. Yet, this slice fails to encompass all intermediate points, indicating a lack of continuity.
Examples of Embeddings
The most straightforward example of an embedding involves positioning a lower-dimensional hyperplane of Rn into Rm, where n < m. The Jacobian of this mapping is simply the identity matrix with additional zeros below. The inclusion map acts as a homeomorphism, confirming its status as an embedding. For instance, the following diagram illustrates the embedding of R² into R³.
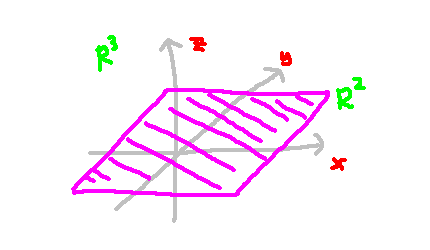
Under certain conditions, immersions can be classified as embeddings, depending on whether the injective immersion ? is a closed map.
Embedded Submanifolds
In this section, we will delve into the local characteristics of subspaces. Can we determine if subspaces are manifolds based solely on their behavior at individual points?
Let’s introduce the concept of an 'embedded k-submanifold.' Similar to tangent spaces, this is defined locally for points in a subset N of a larger manifold M. If for every point p in N there exists a chart (U, ?) for M, allowing us to express U ∩ N as a slice, then N is indeed an embedded k-dimensional submanifold of M.
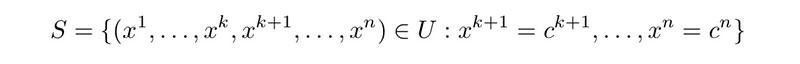
Thus, we establish that N is a manifold of dimension k, possessing a unique smooth structure that allows for the inclusion map N → M to be a smooth embedding. This remarkable finding indicates that subspaces exhibiting nice behavior, akin to slices, are themselves manifolds. Unfortunately, a complete proof of this result is beyond the scope of this article, but I intend to elaborate on it in a future piece.
References
[1] J.M. Lee, Introduction to Smooth Manifolds, Graduate Texts in Mathematics 218, DOI 10.1007/978–1–4419–9982–5_1, © Springer
Chapter 2: Aesthetic Inspiration in Mathematics
The first video titled "Nightfall Musings: LoFi Beats for Late-Night Inspiration" provides a serene backdrop for contemplating mathematical concepts, perfect for late-night study sessions.
The second video, "Nighttime Musings," offers a reflective auditory experience that complements the exploration of complex mathematical ideas.