Exploring Cubic Polynomials: Utilizing Similar Triangles for Roots
Written on
Understanding Similar Triangles in Cubic Polynomials
The application of similar triangles provides a method for estimating roots in polynomial equations, particularly in cubic forms. This introductory piece emphasizes the practicality and straightforwardness of using similar triangle principles in mathematics, specifically within cubic polynomial frameworks.
This technique is especially beneficial for higher-order polynomials, as it can simplify complex calculations, reducing the need for extensive iterations of gradients and height assessments. A more detailed examination of this concept will be covered in a subsequent article. It is assumed that the reader has a high school-level understanding of mathematics.
Concept of Similar Triangles
Similar triangles establish connections across the x-axis between intercept points or nodes, acting as line intercepts on the polynomial function. The proximity of these nodes directly influences the accuracy of root approximation. As illustrated in Diagram 1, similar triangles DEF and GEH yield an approximate root G=E-?x=E-(EH)*DF/EF), which can be compared to Root A, indicated in red.
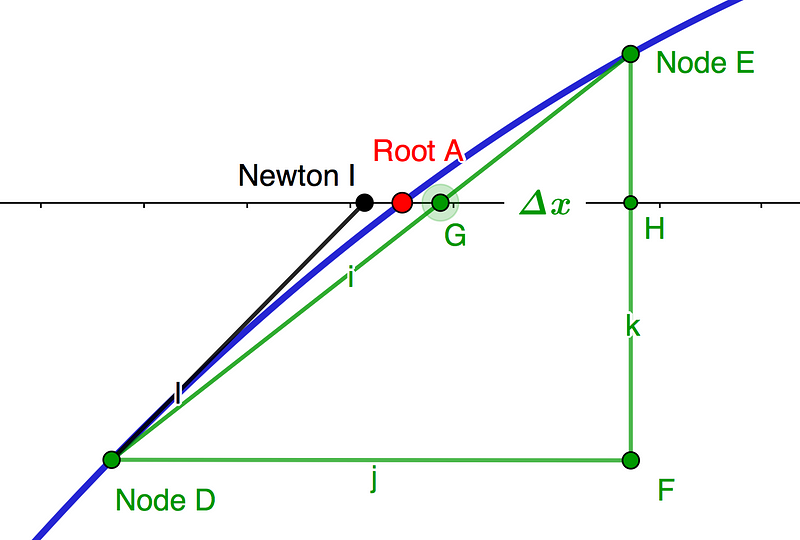
The diagram also visually contrasts Newton’s Approximation Root I, applied from Node D. Unlike some methods that depend on a single point, similar triangles utilize two nodes, D and E, to effectively bracket a targeted root. These nodes can naturally arise in cubic polynomials or be formulated using simultaneous equations via the 'SOSO' method, which employs Same Opposite Same Opposite +/- coefficients.
For further insight, refer to "Quintic Polynomials - Finding Roots From Primary and Secondary Nodes; a Double Shot!" to appreciate the application of SOSO nodes, which range from basic quadratic mathematics to Sextic order. This method allows for flexibility in positioning nodes closer to a desired root, providing the necessary reference points for utilizing similar triangles. Despite requiring an additional node, this approach can often involve less complex calculations than other methods, particularly for higher-order functions with significant concavity or convexity.
Natural Nodes in Cubic Polynomials
Cubic polynomial symmetry presents intuitive methods for deriving simple Turning Point (Tp) and Inflection Point (Ip) coordinates, which can be utilized for natural node derivations. When analyzing cubics with three roots, these nodes consistently straddle the root with the lowest gradient curvature, allowing for accurate approximations.
Example Analysis
Consider the cubic function (y = 2x^3 - 3x^2 - 3x + 4), depicted in blue in Graph 1, with the target Root A exhibiting the steepest gradient and minimal curvature of the three roots. The D intercept aligns with the line Tp(y) opposing turning point F.
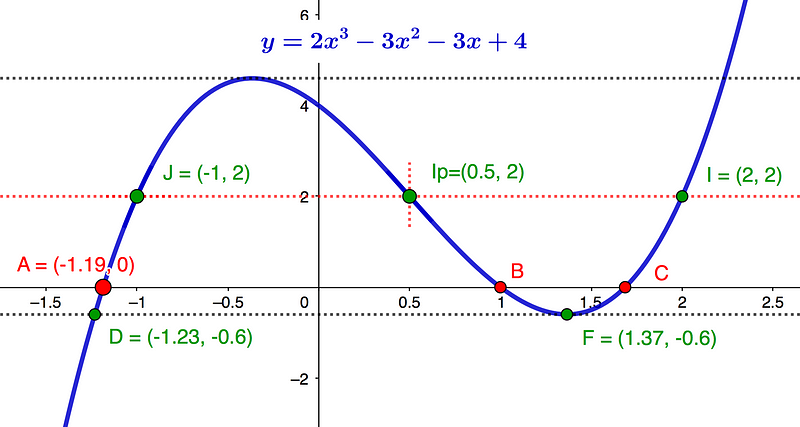
Node J serves as a reference point, calculated using the line (y = 2) through the inflection point (Ip = (0.5, 2)). The calculations proceed as follows:
- Determine (dy/dx = 6x^2 - 6x - 3) and (d^2y/dx^2 = 12x - 6), identifying (Xip = 0.5) and (Yip = 2).
- The sum of the cubic polynomial factors applies similarly to the intercepts on any line (y = h) within the turning point range. This allows us to treat it as a cubic polynomial (y = 2x^3 - 3x^2 - 3x + 2) and utilize the 'Extended Quadratic Equation' for calculating Node J.
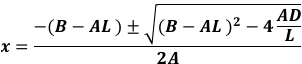
The calculated factor (L = -0.5) leads us to Root J = -1. Meanwhile, Node D is derived from the tangent (y = -0.6) of Turning Point F = (1.365, -0.6) through the same calculus approach. This allows us to approximate Root A at the x-axis intercept by creating a chord from Node D to Node J.
Calculating Root A
A chord connecting Node D to Node J intersects the x-axis at M, depicted in green, and closely approaches Root A = (-1.19, 0), as shown in Diagram 2. The triangle formed by D-J-N effectively shows how closely Root A is approached.
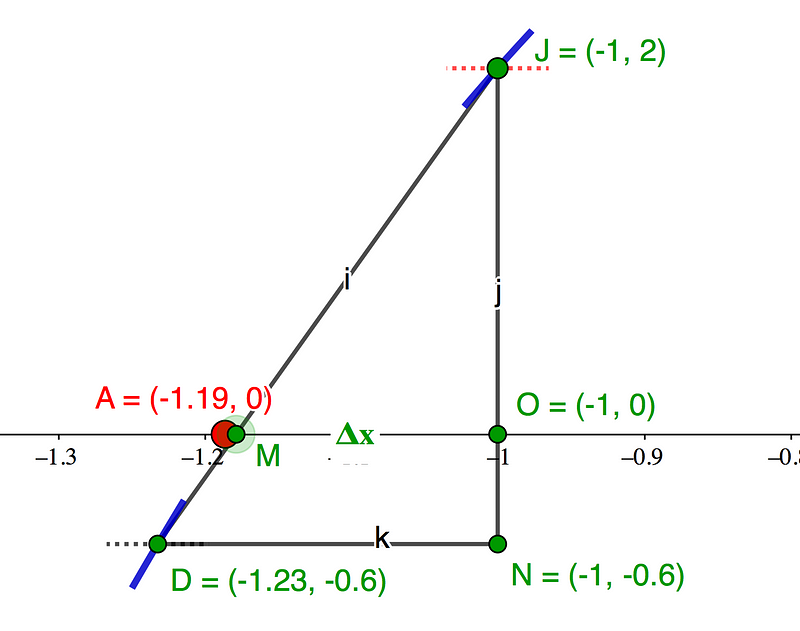
To approximate Root A, the calculation (?x = OJ * {D(x) - J(x)}/(OJ + ON) = -0.18) leads to:
[
text{Approx. Root A} = -1 - 0.18 = -1.18
]
This closely aligns with the actual value of -1.19.
Identifying Remaining Roots
To finalize the analysis, the second and third roots can be easily obtained using the previously mentioned Extended Quadratic Equation.
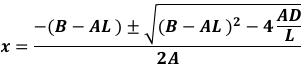
With Factor L = 1.18, we can establish Root B = 1.02 and Root C = 1.66, which compare favorably to the actual values of Root B = 1.0 and Root C = 1.69.
Conclusion
This discussion introduced the use of similar triangles within the framework of cubic polynomials as an effective alternative for root approximation. The goal was to illustrate its potential for broader applications, promoting intuitive learning that connects mathematical concepts with graphical representations, ultimately making mathematics work for the learner.