Discovering the Beauty of Ramsey Theory: Order Amidst Chaos
Written on
Chapter 1: Introduction to Ramsey Theory
Ramsey Theory often emerges through the lens of a colored network. This intriguing branch of mathematics examines the delicate balance between order and randomness. Numerous mathematical fields, including nonlinear dynamics and emergent processes, highlight this phenomenon. Moreover, disciplines such as chaos theory, particularly in the context of our climate, delve into this compelling interplay. In my view, this convergence of math and science is profoundly captivating!
This fascinating boundary can manifest in unexpected contexts, like the rigorously structured realm of Graph Theory. If you're familiar with Graph Theory, you might find this surprising. This mathematical subfield is characterized by strict configurations and highly organized networks. By slightly adjusting the rules, we unearth a vibrant and elegant mathematical domain that navigates the fringes of order and chaos—this is known as Ramsey Theory, named after the remarkable British mathematician Frank Ramsey (1903–1930). Despite his untimely death at the young age of 26, Ramsey's contributions irrevocably transformed mathematics.

Wikipedia provides a poetic definition of Ramsey Theory, describing it as a field of mathematics "that focuses on the appearance of order." While this succinctly captures its essence, it doesn't fully convey the depth of Ramsey Theory, which this article aims to explore. To start, I will introduce the fundamentals of Graph Theory, followed by Ramsey's unique twist involving color. Let’s embark on this mathematical journey!
Section 1.1: Understanding Graph Theory
To grasp Ramsey Theory, we must first familiarize ourselves with Graph Theory, a mathematical field devoted to networks that finds extensive application in computer science. Originally conceived as a whimsical challenge concerning the crossing of bridges, Graph Theory's fundamentals are quite straightforward. It comprises two primary components: nodes and edges, with edges serving to connect various nodes.
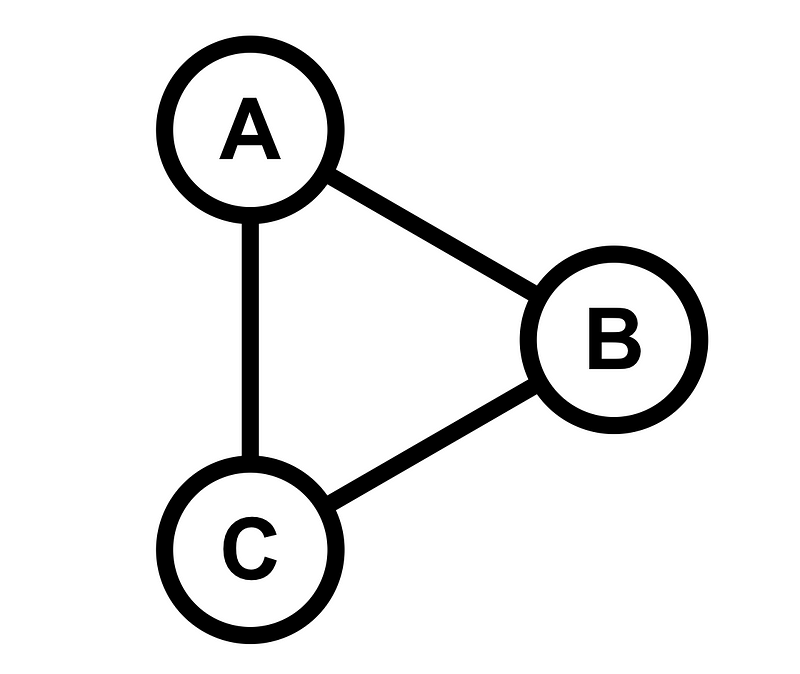
The graph illustrated above contains three nodes and three edges, labeled A, B, and C. This is a specific type of graph known as K3, where all nodes are interconnected. One could visualize a version of this graph where two nodes remain unconnected, which would still be a valid graph but not classified as K3. The subscript indicates the total number of nodes within the graph. Let's take a look at K4 below!
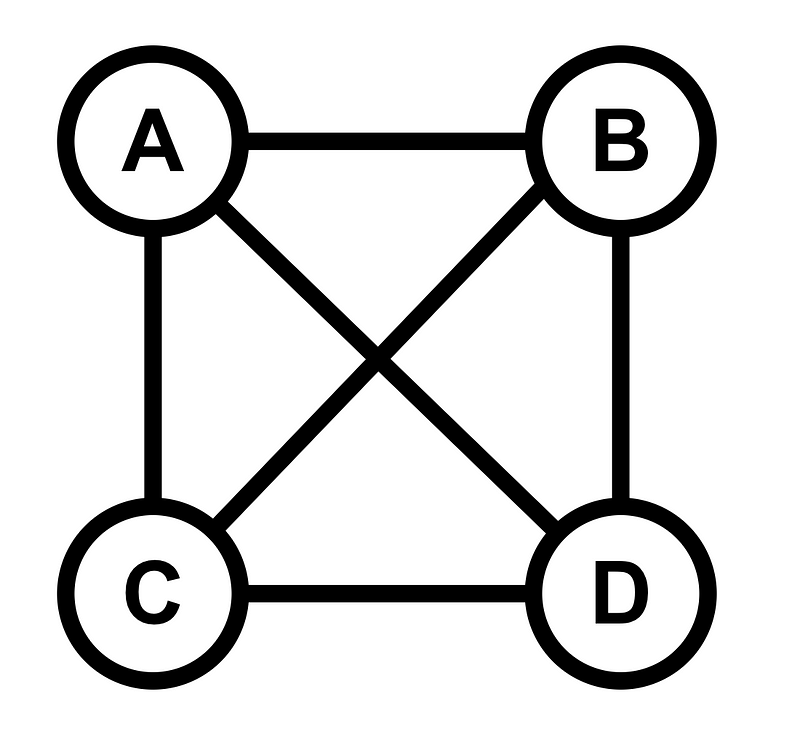
The realm of graphs is nearly limitless. Not every node within a graph must connect to another via edges, making Graph Theory an engaging and versatile discipline. If you wish to delve deeper into the basics, I've authored another article that you can find linked below.
Section 1.2: Transitioning to Ramsey Theory
Having grasped the basics of Graph Theory, we can now venture into Ramsey Theory. To illustrate this, we will introduce various colored edges within our graphs. For simplicity, I will utilize just red and blue edges, although Ramsey Theory can incorporate a wider array of colors.
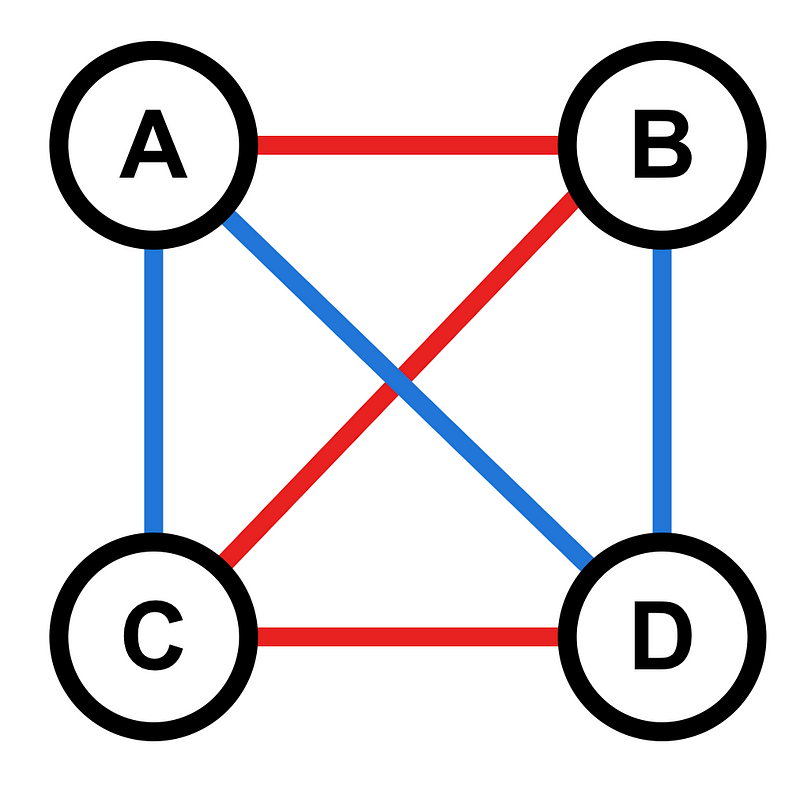
Now that our graph is enriched with color, we can form two distinct subgraphs using only edges of a specific color. Subgraphs are simply smaller versions of the original graph that retain some of its elements. By segregating the edges by color, I have derived two subgraphs illustrated below.
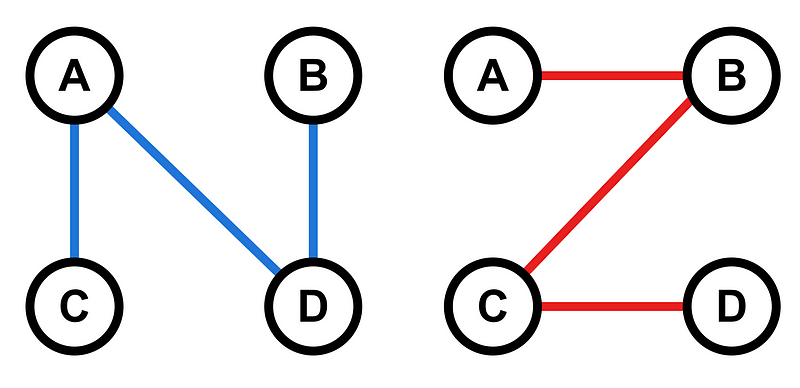
These subgraphs are considered “contained in” the original colored graph, maintaining the same structure but representing a fraction of it. Neither subgraph is complete, as not all nodes are interconnected, unlike the main graph from which they are derived.
Chapter 2: The Power of Ramsey Theory
To demonstrate the effectiveness of Ramsey Theory, let’s consider a playful example. Imagine you invite six friends to a party. Some of these friends know one another, while others do not. This scenario can be depicted with a graph, where each node signifies a person, and colors illustrate their familiarity—blue indicates acquaintances, while red signifies strangers.
This is where Ramsey Theory shines. It posits that, regardless of the scenario, there will always exist a trio of individuals who either all know each other or are all strangers. This assertion seems extraordinary, given the multitude of possible edge arrangements! How can such a fact be established?
The first video titled "Why complete chaos is impossible || Ramsey Theory" further explores these concepts and the underlying principles of Ramsey Theory.
To identify a group of three in the graph where all edges share the same color, let’s take a moment to analyze the connections. There are actually multiple groups of three in this graph. For instance, the nodes A, B, and E are interconnected via red edges, forming a trio of strangers. Another group comprises D, E, and F, connected through blue edges, indicating they are all familiar with one another.
Even with countless configurations of red and blue edges, Ramsey Theory guarantees the presence of at least one such subgroup. In fact, there are 2^6 different arrangements of edges, yielding over 30,000 possibilities! It's fascinating that, despite the variety, there will always be at least one group of three individuals who are either all acquaintances or all strangers.
The second video titled "Ramsey Theory - finding order in chaos and graphs" elaborates on how Ramsey Theory uncovers order within chaotic systems.
Upping the Complexity
The example above revolves around a relatively simple graph with just six nodes and two edge colors. What we've computed is referred to as a Ramsey Number, denoted as R(3, 3). The two threes indicate the size of the smaller groups we’re examining. Since we were searching for either a red or blue group of three, both numbers are identical. Consequently, we conclude that R(3, 3) = 6, meaning if we gather six people at a party, there will inevitably be a trio that either all know each other or all do not.
Mathematicians have determined that R(4, 4) = 18, suggesting that if we invite 18 guests, there will always be a subgroup of four who are either friends or strangers. Interestingly, R(5, 5) remains an enigma, known only to lie between 43 and 48 attendees.
The complexity of calculating Ramsey Numbers increases dramatically with larger graphs. Consider a graph with 43 nodes—there are 2^43 possible arrangements of colored edges! This staggering number far exceeds a googol multiplied by a googol, where a googol is defined as the number 1 followed by one hundred zeros. Even the most advanced supercomputers would struggle to compute every potential arrangement within a timeframe shorter than the universe's age.
Mathematicians have developed various ingenious methods to estimate these numbers, which is why we have a range of approximations. The proofs behind these calculations delve into advanced topics beyond the scope of this article, but I’ve included some references for those interested.

Ultimately, Ramsey Theory reveals that amid randomness, some level of order will always manifest. This powerful insight can be applied across numerous domains.
Going Further
I hope this exploration has enriched your understanding! Ramsey Theory is indeed a captivating mathematical subfield, and many unsolved theorems continue to challenge mathematicians today. For those eager to delve deeper, I have included several resources below.
If you seek an online tool for creating your own graphs, I highly recommend csacademy or yEd, the latter of which I utilized for this article. For textbooks, "Introduction to Graph Theory" offers a comprehensive overview of the subject and is quite affordable. Alternatively, "An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics" is a standard resource on Ramsey Theory, while free online notes provide a more accessible introduction. Lastly, D3 Graph Theory is an interactive site that teaches the fundamentals of graph theory.
If you enjoyed this article, consider giving it a clap! You might also want to follow me for more insights or subscribe to my email list, where I share weekly content on mathematics and science.