Exploring Advanced Queues in JavaScript: A Comprehensive Guide
Written on
Chapter 1: Introduction to Custom Data Structures
In addition to the six fundamental data structures, JavaScript allows for the creation of custom data structures tailored to specific needs.

Photo by Adrien Olichon from Pexels | Edited by Author
As JavaScript continues to evolve, its applications expand significantly. Unlike in 2007, modern JavaScript can even be used to control drones, showcasing its versatility. However, back in 1995, JavaScript was not designed for such advanced tasks, leading to its lack of support for more complex data structures. This series will explore the data structures and algorithms within JavaScript by creating custom structures and applying them in problem-solving scenarios. Below is a look at stack implementation.
Stacks: A Deeper Look into JavaScript Data Structures
While JavaScript has six built-in data structures, it also supports the creation of custom ones.
What Is a Queue?
A queue is a linear data structure that stores values and allows them to be processed in a specific manner. With a time complexity of O(1), the length of the queue does not influence its complexity.
A basic queue consists of three core operations: enqueue, dequeue, and front. Additionally, I will introduce some helper methods to enhance its functionality.
FIFO Principle
The queue operates on the First In First Out (FIFO) principle, meaning the first item added to the queue will be the first to be removed. This straightforward mechanism allows for items to be added sequentially and retrieved in the same order.

Let’s Implement It
There are various ways to implement a queue in JavaScript, including linked lists, pointers, or arrays. In this guide, I will demonstrate a simple implementation using an array along with essential and helper methods.
Begin by creating a Queue class, where the constructor accepts a named parameter for capacity, indicating how many items the queue can hold. This capacity is optional.
3 Marvelous JavaScript Tips to Speed Up the Development Process
After defining the constructor, establish the class properties. Create a private property for capacity and another for the queue itself. If no capacity is defined, the queue will default to an infinite capacity for flexibility.
Now, let’s define three more methods in the Queue class: enqueue, dequeue, and front.
The enqueue method allows adding items to the queue as long as it isn’t full. If an attempt is made to add more items than the defined capacity, it will throw an "Overflow!" error. To facilitate adding multiple values at once, the rest operator will be utilized.
The dequeue method removes elements sequentially from the front of the queue. If there are no items to dequeue, it will raise an "Underflow" error.
The front method simply returns the first element in the queue without altering the queue’s state.
With these methods in place, you now have a functional queue to incorporate into your projects. For added utility, I’ve included six additional helper methods in my version, which can be found in the repository.
Queue in Action: Solving a Chess Problem
To demonstrate the utility of the queue we’ve created, we will tackle an algorithmic problem. In chess, the knight moves in an "L" shape. Our goal is to calculate the minimum steps required for the knight to move from a source point to a destination.
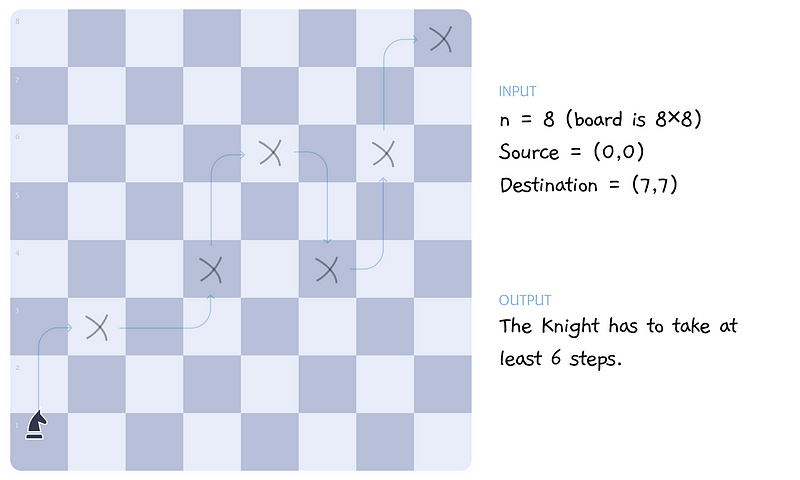
If implemented correctly, the program should indicate that the knight takes six steps to reach from (0, 0) to (7, 7).
To achieve this, we will employ the Breadth-First Search (BFS) algorithm, which assesses each possible knight position and stores them in the queue. By dequeuing these positions, we can determine the knight's next move.
Let’s create a function called findShortestStep, which takes the source point, destination point, and the board dimensions as arguments. We will instantiate our queue without passing any arguments, allowing it to have an infinite capacity for storing positions.
Next, we will set up two 2D arrays to track the knight's path and move count.
The knight can move to eight different positions from its current location, provided it is not near the edge of the board.
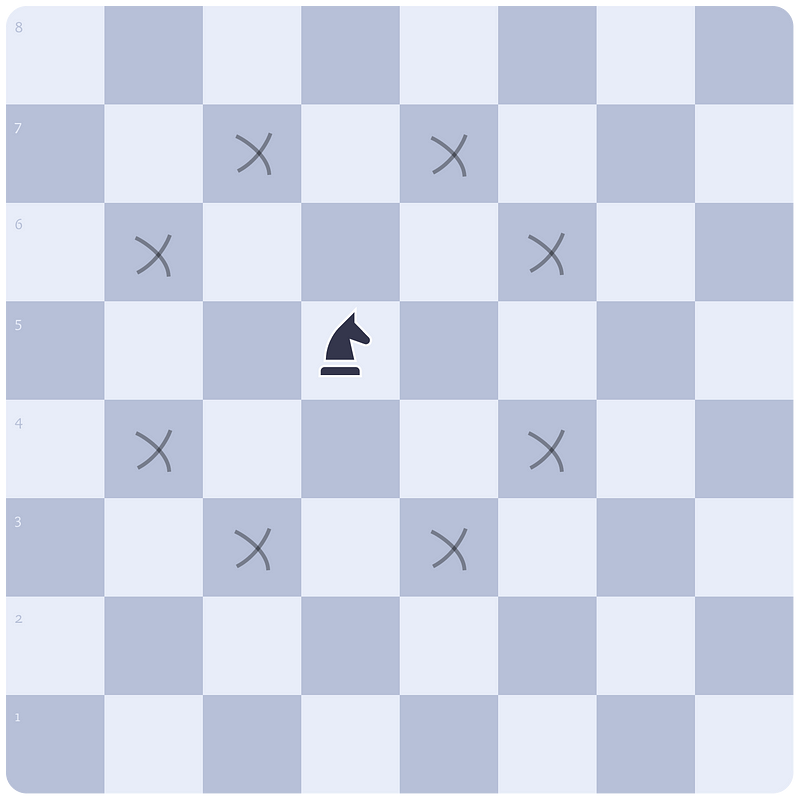
We will create an object representing these potential moves based on the knight's initial position.
Finally, we will finalize our function setup and focus on implementing the BFS algorithm as follows:
- Dequeue the last visited node.
- If the dequeued position matches the destination, exit the loop and return the distance.
- Otherwise, calculate the potential moves and mark them as visited.
- For each of the eight possible moves, enqueue the new position with an increased distance.
- Repeat steps 1-4 until the queue is empty.
To start, we will mark the source point as visited and enqueue it, then use a while loop to iterate through these steps.
As noted, there are several utility functions and methods of the queue that have yet to be implemented. In my repository, a more advanced version of the queue includes additional methods such as isEmpty. Be sure to check it out for further details.
When we run our function with the given parameters, it should return six as the number of steps required.

Conclusion
Congratulations! You have successfully implemented a queue in JavaScript and utilized it to solve a practical problem. This is just the beginning; stay tuned for future episodes where we will explore linked lists, binary trees, graphs, and much more.
Subscribe to gain access to exclusive content for subscribers. If you enjoyed this article, please show your support, and feel free to share your thoughts in the comments. Until next time!
The first video, "Deep Dive into the Queue Data Structure," offers an in-depth look at queues, explaining their importance and various implementations.
The second video, "Data Structure Queue in Javascript - Learn the Algorithm," provides a practical guide to implementing queues in JavaScript, focusing on algorithms related to this data structure.